Computing sequential games: solution
Introduction
In my last post, we represented a sequential game of complete and perfect information as a trie. In this post, let's solve that game!
Setup
Let's assume the following:
- The players act economically rational; they care only to maximize their own utility/payoff.
- No two possible combinations of moves yield the same exact utility/payoff for the same player.
With these assumptions, our sequential game of complete and perfect information must have a single deterministic outcome. To reach this outcome, we can use backward induction, from game theory.
To traverse our trie elegantly, we can use recursion, from computer science.
Solution
Let's describe the solution in Python (3.9):1
from __future__ import annotations
from dataclasses import dataclass, field
from typing import Any, List, Mapping, Optional, Tuple
@dataclass
class GameTrie:
possible_moves: Mapping[Any, GameTrie] = field(default_factory=dict)
outcome: Optional[Tuple[float]] = field(default=None)
move: Optional[Any] = field(default=None)
def insert_outcome(
combination_of_moves: Tuple[Any],
outcome: Tuple[float],
game: GameTrie,
) -> None:
current_game = game
for move in combination_of_moves:
if move not in current_game.possible_moves:
current_game.possible_moves[move] = GameTrie()
current_game = current_game.possible_moves[move]
current_game.outcome = outcome
def solve_game_impl(
game: GameTrie,
player: int,
) -> None:
player_outcomes = {}
for move, sub_game in game.possible_moves.items():
if sub_game.outcome is None:
solve_game_impl(sub_game, player + 1)
assert (sub_game.outcome is not None)
player_outcome = sub_game.outcome[player]
player_outcomes[move] = player_outcome
# get move associated with max player outcome
best_move = max(player_outcomes, key=player_outcomes.get)
game.move = best_move
game.outcome = game.possible_moves[game.move].outcome
def solve_game(game: GameTrie, ) -> Tuple[Tuple[Any], Tuple[float]]:
solve_game_impl(game, 0)
moves = []
current_game = game
while current_game.move is not None:
moves.append(current_game.move)
current_game = current_game.possible_moves[moves[-1]]
return moves, game.outcome
We can test this code against this example game from Investopedia:
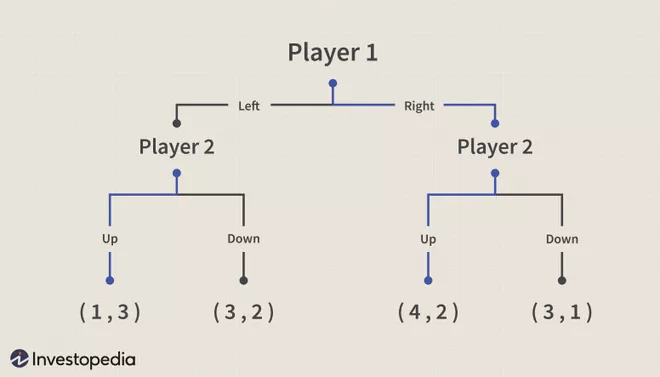
...
def print_pre_order_impl(
trie: GameTrie,
moves_so_far: List[int],
) -> None:
print("-" * 30)
print(f"Moves so far: {moves_so_far}")
print(f"Outcome: {trie.outcome}")
print(f"Move: {trie.move}")
for move, sub_trie in sorted(trie.possible_moves.items()):
print_pre_order_impl(
sub_trie,
moves_so_far + [move],
)
def print_pre_order(trie: GameTrie, ):
print_pre_order_impl(trie, [])
if __name__ == "__main__":
game = GameTrie()
insert_outcome(combination_of_moves=("Left", "Up"),
outcome=(1, 3),
game=game)
insert_outcome(combination_of_moves=("Left", "Down"),
outcome=(3, 2),
game=game)
insert_outcome(combination_of_moves=("Right", "Up"),
outcome=(4, 2),
game=game)
insert_outcome(combination_of_moves=("Right", "Down"),
outcome=(3, 1),
game=game)
moves, outcome = solve_game(game)
print(f"Moves: {moves}")
print(f"Outcome: {outcome}")
print("\nTrie:")
print_pre_order(game)
which gives us output:
Moves: ['Right', 'Up']
Outcome: (4, 2)
Trie:
------------------------------
Moves so far: []
Outcome: (4, 2)
Move: Right
------------------------------
Moves so far: ['Left']
Outcome: (1, 3)
Move: Up
------------------------------
Moves so far: ['Left', 'Down']
Outcome: (3, 2)
Move: None
------------------------------
Moves so far: ['Left', 'Up']
Outcome: (1, 3)
Move: None
------------------------------
Moves so far: ['Right']
Outcome: (4, 2)
Move: Up
------------------------------
Moves so far: ['Right', 'Down']
Outcome: (3, 1)
Move: None
------------------------------
Moves so far: ['Right', 'Up']
Outcome: (4, 2)
Move: None
Conclusion
A correct solution to our game! What a wonderful intersection between game theory and computer science! For more, search for combinatorial game theory.
Note unlike in other math, indices in Python begin at 0, not 1 ↩︎